Sigmund, Ole. "A 99 line topology optimization code written in Matlab." Structural and multidisciplinary optimization 21 (2001): 120-127.
Before explaining the paper, I would like to start with some basic information about optimization.
Optimization, simply put, is the process of finding a solution that minimizes or maximizes an objective function while satisfying a set of constraints.
Structural optimization, a type of optimization, refers to the design technique that applies optimization theory to the design of structures to achieve superior performance or economic benefits compared to existing designs.
Structrual optimization can be broadly divided into three categories: Size optimization, Shape optimization, and Topology optimization.
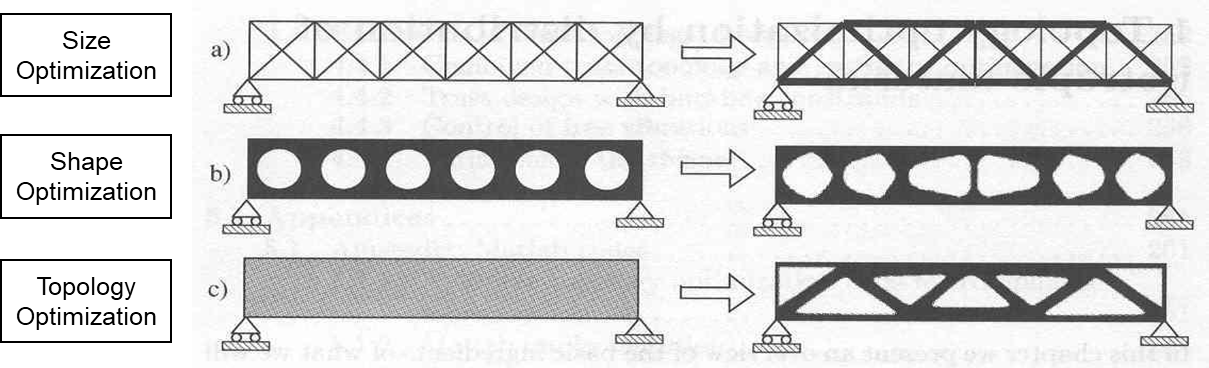
To overcome the disadvantages of size optmization and shape optimization, which are highly dependent on the initial design, structural optimization problems were approached as material distribution problems. Subsequently, through the density method, the design domain is discretized into a finite number of elements, treating the material density of each element as a design variable and handling it as a continuous variable. Due to its ease of implementation, it is widely used in the design for lightweight products.
Now, let's proceed to explain the content of the paper.
Abstract
The paper provides a simple MATLAB code implementation for the problem of minimizing compliance in topology optimization, contained within just 99 lines. The MATLAB code presented can be downloaded from http://www.topopt.dtu.dk
Introduction
Various approaches to solving topology optimization problems can be found in numerours publications. Bensoe and Kikuchi sought to address the topology optimization problem though a microstructure or homogenization-based approach.
The homogenization-based approach is widely used in many papers, but it has the disadvantage of being complex in determining and evaluating the optimal microstructure and its orientation when solutions are not readily available. However, it is important bacause it can provide limits on the theoretical performance of structures.
This paper is organized into sections on the definition of the optimization problem, MATLAB implementation, extensions, and concolusions.
Topology optimization problem
First, for the simplification of the MATLAB code, a rectangular design domain is assumed and discretized by square finite elements, The aspect ratio of the structure is given by the element ratio of ${\text{nelx}}$ and ${\text{nely}}$.
The object function is compliance, the constraint is the volume fraction, and the design variable is the element density.
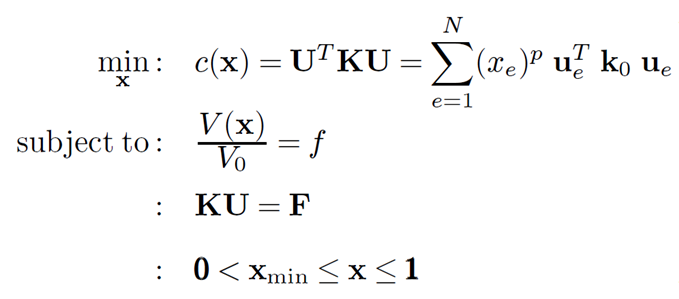
Where ${\text{U}}$ and ${\text{F}}$ represent the global displacement and force vector, respectively, ${\text{K}}$ is the global stiffness matrix, ${u_e}$ and ${k_e}$ are the element displacement vector and elemtn stiffness matrix, respectively, ${\text{x}}$ is the design variable vector and ${{\text{x}}_{\text{min}}}$ is the minimum density vector to solve numerical instability. $N$ is the number of elements used to discretize the design domain and is equal to ${\text{nelx}} \times {\text{nely}}$. $p$ is the penalization power, typically using a value of 3, $V({\text{x}})$ and ${V_0}$ are the material volume and the volume of the design domain, respectively, and $f$ is the prescribed volume fraction.
Furthermore, the Optimality Criteria (OC) method was used to solve the optimization problem, and it can be formalized as follows.
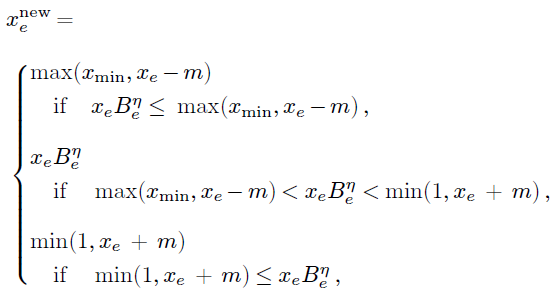
Where $m$ is the move limit, and $\eta $ is the numerical damping coefficient. Therefore ${B_e}$ is defined as follows.
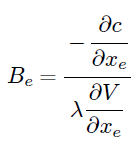
Where $\lambda $ is the Lagrangian multiplier, which can be found using bi-sectioning algorithm.
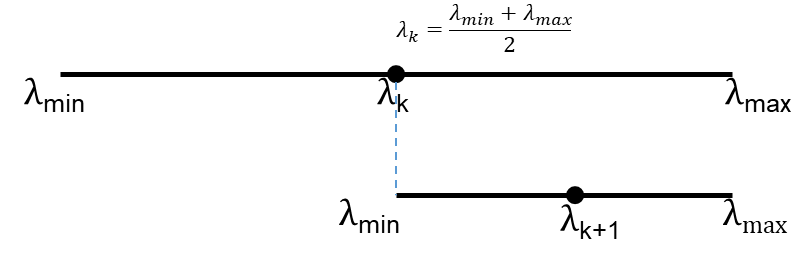
The above equation can be derived through the following mathematical process.
Lagrangian function with KKT condition

The sensitivity of the objective function is as follows.
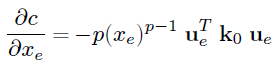
It can be derived through the following process.
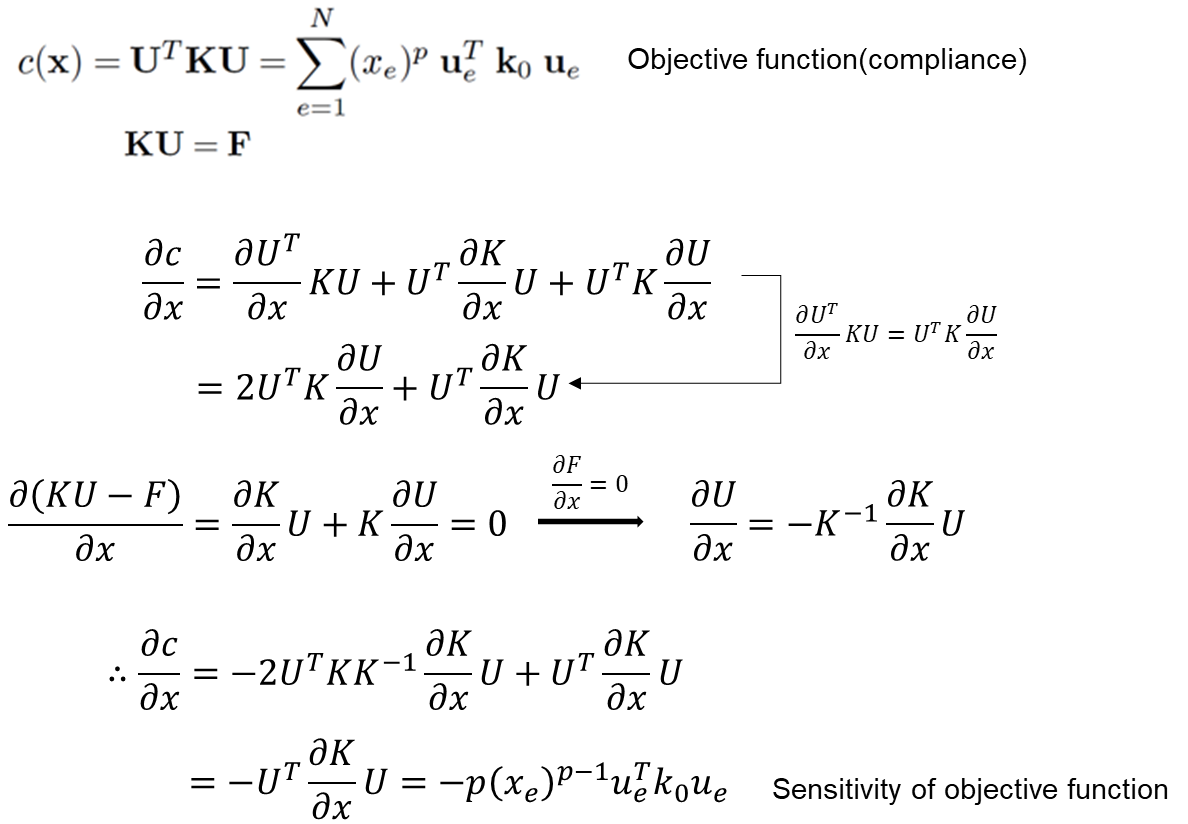
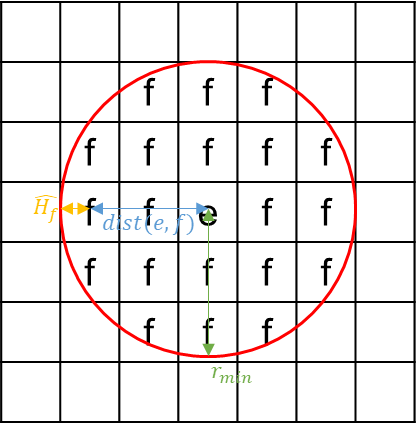
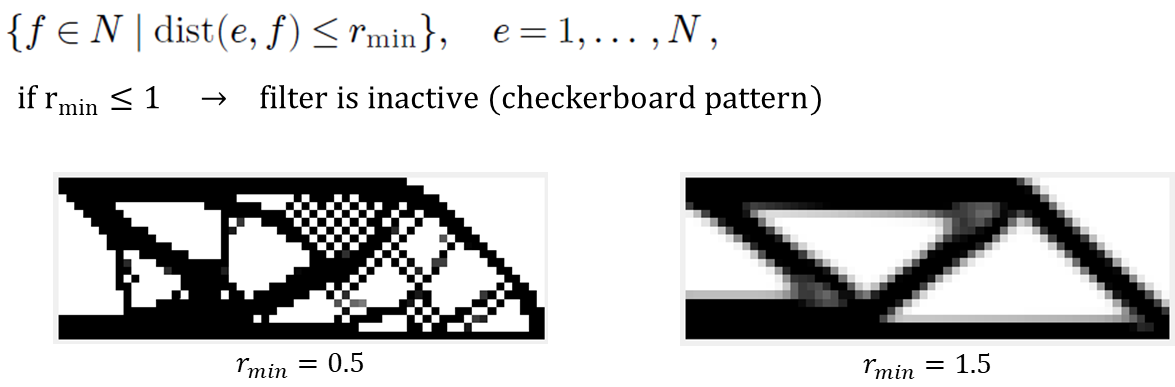
Additionally, filtering technique was employed to address the checkerboard phenomenon, and a mesh-independency filter that works by modifying the element sensitivities was used.
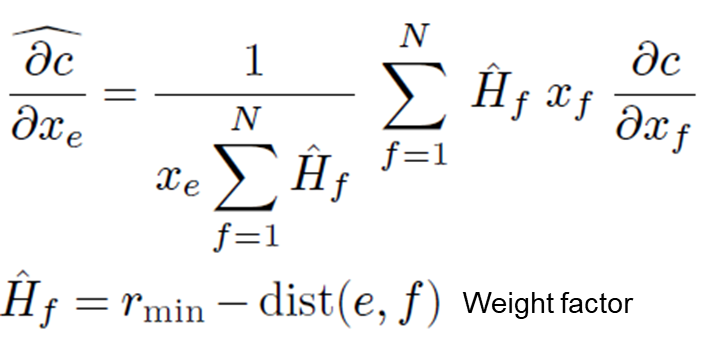
Where ${\text{dist}}(e,f)$ represents the distance between the center of element $e$ and the center of element $f$.
MATLAB implementation
The inputs required are the numberof elements along the horizontal axis (${\text{nelx}}$), the number of elements along the vertical axis (${\text{nely}}$), the volume fraction, the penalization power($p$), and the filter radious (${r_{\min }}$), totaling five inputs.
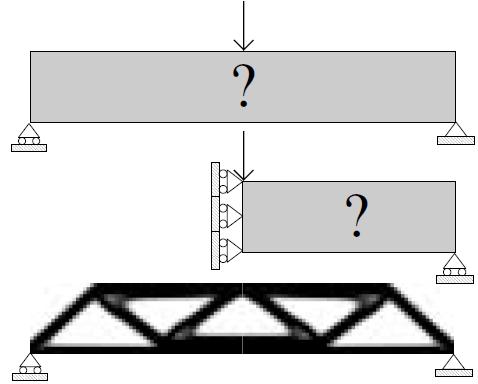
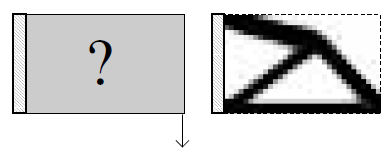
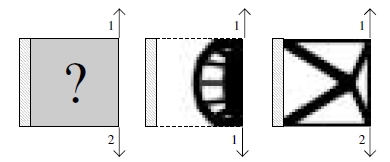
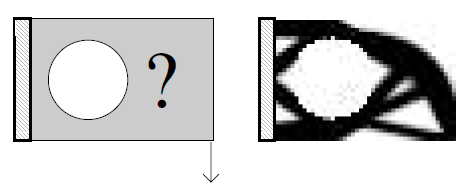
As demonstrated in the examples above, the code can be modified to set various constraints.
This paper encompasses the fundamentals and most crucialaspects of topology optimization and provides code, making it a very important and helpful resource for studying topology optimization.